ダミーのための惑星と衛星の動き
2015 年 5 月 6 日午後 4 時 10 分科学
こんにちは、若いホモサピエンスよ、あなたは惑星に住んでいることを知っていますか?はい、もちろんキャプテン・オブビアスには感謝しますが、これが動くことを知っていましたか?オブビアス船長、2回目ありがとうございます!それがどのように動くのか、その動きの特性は何なのかを疑問に思ったことはありませんか?そうです、惑星や衛星は思い通りに動くわけではなく、規則に従っているので、私はそれを説明するためにここにいます。まず、過去に戻ります (Code Lyoko を知っている場合など)。そして、すぐに Bac の小さなビデオレビューを始めます。

ケプラーの法則
1571 年にヨハネス ケプラーが生まれました。彼は、ターミナル S の同僚が尊敬するに違いない有名な天文学者であり物理学者です。ケプラーは長い研究の末、そのような天体の性質は見つからないので、1609 年と 1618 年に 3 つの法則、つまり軌道の法則、面積の法則、周期の法則を実証しました。
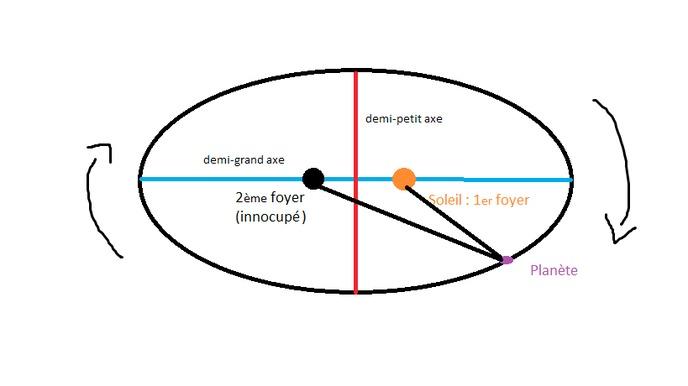
ケプラーの第 1 法則: 軌道の法則
まあ、当時、私たちは完全に愚かではなかった、私たちは地球が丸いこと、太陽が太陽系の中心であり、惑星がその周りを公転していることをすでに知っていました(少なくとも私たちが知っていた惑星)、しかしこれらの軌道は完全な円であると考えられていました。そこでケプラーは、惑星は円形の軌道をたどるのではなく、楕円形の軌道をたどるという軌道の法則を実証することで、当時の天文学に一石を投じました。
私たちの太陽系の各惑星は太陽の周りに楕円を描いており、その中心の 1 つは太陽であり、もう 1 つは空いています。
ケプラーの第 2 法則: 面積の法則
この当時としては驚くべき発見を受けて、ケプラー氏は、楕円の移動、つまり惑星が覆う距離と表面に特に興味を持つようになりました。私の壮大なペイント図面には、太陽だけでなく、異なる時間の惑星を表す 4 つの点が表示されます。法則によれば、惑星と太陽を結ぶ光線は、同じ期間、同じエリアを通過します。
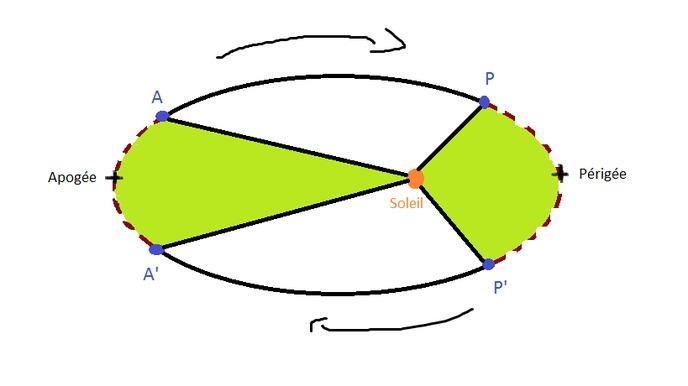
これを表すには (太陽は文字 S で表されます):
光線のSP、SP'、SA、SA'を載せます
SPP' = 期間 T にわたって惑星が通過する面積
SAA' = 期間 T' にわたって惑星が通過する面積
そこで私はここであなたの科学的論理に訴えます。私たちのコミュニティが知的であることを示してください。
1 - T と T' が等しい場合、面積は等しい。
2 - T と T' が等しい場合、円弧 PP' の面積は必然的に円弧 AA' の面積より大きくなります。したがって、P と P' の間の速度は、A と A' の間の速度よりも大きくなります。
彼の観察と結果のおかげで、惑星の速度は、惑星が太陽に近づくと速くなり、太陽から離れると遅くなることが推測できます。。したがって、惑星は近地点で最大速度に達し、遠地点で最小速度に達するため、この動きは均一ではありません。
この法則から、地球に働く力は常に太陽の方向に向いていると言えます。
この法則を使用した具体例として、冬は 89 日、夏は 93 日など、季節の長さが異なる理由を解明することができました。
ケプラーの第 3 法則: 周期の法則
そして最後に、最も待望され、最も求められている最後の法則は、数学的順序に従って軌道、つまり惑星の公転周期を定義することを可能にするものです。注意: 公転周期と惑星固有の周期を混同しないでください。公転周期は、惑星が太陽の周りを楕円形に移動するのにかかる時間であり、適切な周期は、惑星がその軸の 1 つの周りを完全に回転するのにかかる時間です。(自転する地球)。
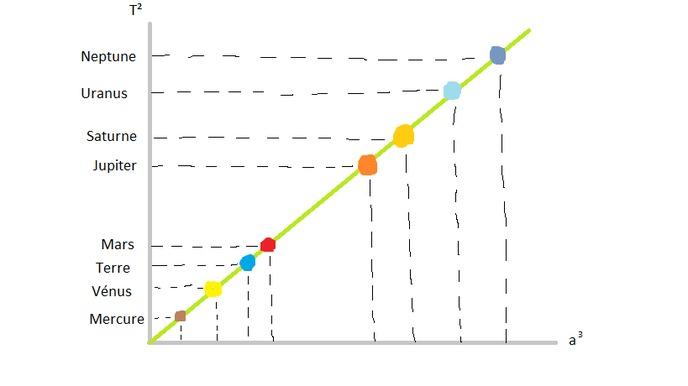
地球には長半径 = 149597887.5 km があることはわかっています (ありがとう、主様 Wiki)。したがって、ケプラーの公式を適用すると、地球の公転周期はおよそ 366 日であることがわかります (365 日であることはわかっていますが、データはおおよそのものです。文句は言わないでしょう)。
したがって、応用例は数多くあり、特に次のような確実性を表現できるようにすることで、当時の天文学を大幅に進歩させました。太陽から最も遠い惑星は最も速度が遅かった。
衛星化
「わかりました、あなたの複雑な法律はすべてうまくいきますが、それは私が何かを軌道に乗せる方法ではありません。」忍耐強く、若いリンゴ、これはこれからやってくる知識です。
物体を地球に接続する主な力は地球の引力です。それは簡単です。空中にジャンプすると、地球の引力のおかげで後退します。衛星を軌道に乗せてテレビや番組を一気に視聴できるようにするには、地上から打ち上げられるロケットに衛星を乗せます。これは離陸にエンジンを使用します。ちなみに、私たちはこの現象をジェット推進と呼んでいます。エンジンは大量のガスを非常に高速で噴射し、地球の重力に対抗できる推力を生み出します。
押される力とは何かを説明するための小さな例です。なぜなら、あなたが私の図を気に入っているのはわかっているからです。
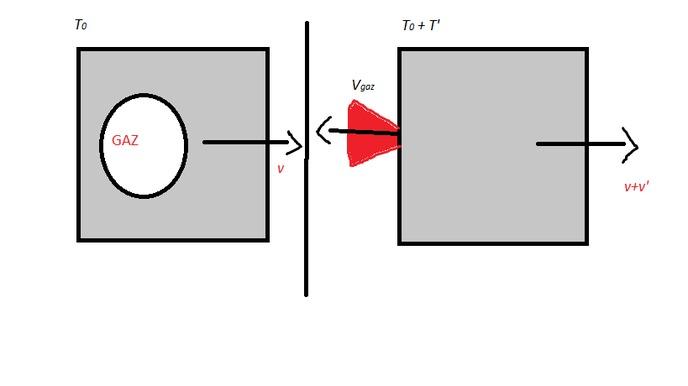
太陽系から遠く離れ、重力からも遠く離れた探査機を想像してみましょう (1977 年のボイジャー 1 号と 2 号探査機)。質量 M 、時刻 t0 の速度 v のプローブは、持続時間 T' にわたってその質量の一部をガスの形で速度 Vgas で放出します (鼓腸のときのように)。時間 T+T' におけるプローブの速度は V+V' に等しい
この押す力は、排出されるガスの速度と質量流量に比例します (2 回目のおならのときなど)。 Fp = Dgas x Vgas。これまでのところ、ロケットは離陸し、推力の方が大きい場合は地球の引力を克服し、衛星を放出する準備をしています。しかし、この衛星が機能し、地球に墜落したり、宇宙で紛失したりしないようにするにはどうすればよいでしょうか?

衛星は星の周りを一定の速度で回転します。一般に信じられていることに反して、衛星は無重力ではありません。常に自由落下しているにもかかわらず、その速度のおかげで地球の「隣」に落ちます。空気摩擦がなければ、もちろん障害物を避けながら、どの高度でも軌道を周回することができます。しかし、大気のせいで高度200km未満に衛星を設置することはできない。なんて制限のある惑星なんだろう。この低空に設置された衛星は数日しか持たないでしょう。空気によってブレーキがかかると速度が低下し、地球に帰還します。衛星に与えられる速度は高度に応じて低下します。高ければ高いほど、重力の影響を受けにくくなります。衛星速度は 200 km で 8 km.s、2000 km で 6.9 km.s です。
したがって、この記事が気に入っていただき、宇宙の動きや天体力学についてもっと学び、私のおかげで皆さんが将来の宇宙エンジニアになってくれることを願っています。私が説明していない点や、あなた自身が疑問に思っている点について、遠慮なくコメントで質問してください。
PS: 興味のある方のために、かなり役立つ数式をいくつか紹介します。






